Les opérations à trous démystifiées par une méthode originale d’apprendre les maths aux enfants

 

Qui n'a pas buté sur une opération à trous lors de ses années d'école ?

Véritables tests de compréhension, ces opérations sont souvent à l'origine de blocages, de frustrations et de perte de confiance.

Des élèves ayant appris à résoudre avec succès  « 9 = 7 + … » finissent, quinze jours plus tard, par additionner  9 et 7 !

J’avais soumis cette opération à une bonne vingtaine d’enfants initiés depuis longtemps au bon usage des doigts : pas une seule erreur !

La difficulté ne réside donc pas dans l'opération en elle-même, mais dans la manière dont elle est présentée ?

L'enseignement traditionnel éloigne trop souvent les jeunes enfants des maths vivantes

•   Il méprise leur environnement familier, leur potentiel  mathématique et leur matériel (les doigts).
•   Il les dégoûte par des pseudo-problèmes destinés à appliquer des abstractions. 
•   Il traite d’incapables ceux qui ne s’adaptent pas dûment à ses artifices. Il s’immunise ainsi contre toute autocritique et contre tout progrès.

Une méthode novatrice d’enseigner les maths : conduire à la réussite tous les enfants en respectant :

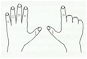
•  leur matériel mathématique : les doigts. Ceux-ci sont LE « matériel » idéal pour une entrée triomphale en mathématiques.
• leurs problèmes : même les plus jeunes peuvent se confronter à des problèmes qui les intéressent  et qu’ils savent résoudre. Sans vrais problèmes, pas de maths vivantes. (2)
•  leur potentiel mathématique insoupçonné : tout enfant, jugé capable d’être scolarisé et obligé de l’être, est aussi capable de construire le nombre et la calculatrice-doigts avec ses configurations canoniques (CCD). (3) Grâce à cette calculatrice l’enfant peut résoudre les problèmes et faire des progrès époustouflants en maths.

La démystification des opérations à trous, un tremplin vers la réussite en maths. 

Les CCD de 5 et de 4 ne sont pas extérieures à la CCD de 9

Ta copine a 9 poupées. Elle a seulement 5 robes. Problème : CALCULE combien de robes elle doit encore acquérir. L’enfant prend la CCD de 9 ou plus rarement celle de 5 et « voit » (il peut faire l’exercice à l’aveugle, la proprioception étant très importante) D’UN SEUL COUP la solution. Il peut vérifier la fiabilité de la calculatrice  avec des poupées réelles, avec des jetons les représentant ou avec les deux.

L’enfant est ainsi d’emblée délivré du comptage usurpant la place du calcul et de la peste du « ça fait » défigurant totalement le signe =.

Ce n’est que quand l’enfant excelle dans la résolution des problèmes les plus divers, qu’on peut introduire les abstractions : 5 + . = 9 ; 9 - 5 = . ; 9 = 5 +. ; 5 = 9 -. ;  . = 9 - 5. Toutes les opérations sont à trou, peu importe l’endroit de ce dernier!

Le + est la colle qui colle ensemble les parties et se trouve donc toujours entre elles. Le -décolle une partie de la totalité qui se trouve juste devant. Plus tard encore, apparaîtra le x comme super-colle.

Découvrez comment les doigts peuvent devenir votre meilleur outil pour transmettre les maths !

 

Vous en avez assez de voir vos élèves bloqués sur les additions, les soustractions ou les tables de multiplication ?

👉Une méthode simple et efficace existe pour les aider à surmonter ces difficultés et à déjouer les nombreux pièges qui en sont l'origine (le numéro à la place du nombre, le comptage à la place du calcul, etc.).

 Grâce à une technique innovante, les "Configurations Canoniques des Doigts" (CCD), vous apprendrez à visualiser et à vivre  les nombres et les opérations de manière intuitive.

Les avantages des CCD :

• Outils par excellence pour la construction du nombre conçu comme synthèse entre l’aspect ordinal (premier, deuxième, troisième,…) et cardinal (un, deux, trois,…)
• Alliance entre le concret et l’abstrait : les enfants gardent leurs pieds sur terre sans être empêtrés dans un concret encombrant.
• Repères clairs, stables et fiables. Fini le stress, bannie l’angoisse de se perdre dans une jungle impénétrable
• Accessibilité optimale : chaque enfant, du plus riche au plus pauvre, dispose à tout moment gratuitement de ses doigts. 
• Mémorisation et automatisation allant de soi grâce à l’apprentissage par le cœur, par le corps, par les doigts.
• Efficacité éprouvée : Les résultats sont rapides et durables.
• Source de satisfaction, de joie et de bien-être. L’enfant découvre avec d’autant plus de plaisir les potentialités de son corps, de ses doigts, que ses activités sont couronnées de succès et de réussites.  
• Adaptabilité : La méthode s'adapte à chaque enfant de tous les niveaux, des Maternelles au début des secondaires. Elle convient aux enseignants ainsi qu’à tous ceux et toutes celles qui aident les enfants dans leur apprentissage des mathématiques.
• ...

Les témoignages de nos utilisateurs parlent d'eux-mêmes:

•  « Mes élèves de 1ère année calculent avec une facilité déconcertante… et tous y arrivent ! Grâce à votre méthode, j’ai moi-même l’impression  de mieux savoir où je vais… ».  Institutrice
• « J’ai essayé avec des enfants de CE2 qui avaient du mal dans les calculs et j ai vu de suite l’intérêt des ccd, et leur impact bénéfique pour sortir du carcan des représentations chiffrées symboliques, du comptage et le levier pour le lien entre ordinal et cardinal. C’est aussi un bon moyen de privilégier les images mentales efficaces pour le calcul et apprendre la flexibilité. » - Psychopédagogue
• Les DOIGTS utilisés correctement (en construisant des configurations "cardinales" et non en restant dans le comptage) reste le plus naturel des "outils" pour aborder le nombre et les opérations (gratuit et toujours à portée de main). Je recommande vivement le livre de Ewald Velz à ce propos. - Orthophoniste/logopède

Rejoignez-nous pour découvrir cette méthode révolutionnaire de transmettre les mathématiques! 

Où ? Athénée Royal François Bovesse, rue du Collège, 8, 5000 Namur

Quand ? Mercredi 21 août de 13h15 à 14h30

Inscription : https://www.sbpm.be/congres/congres2024/inscription/"

Faites profiter les enfants de la force du nombre 5

 

Le nombre 5 et la Configuration Canonique des Doigts (CCD) de 5 qui le désigne jouent un rôle capital dans l’entrée réussie en mathématiques.

Certains commencent même par le nombre 5 ! Ce que je déconseille. Cela est d’ailleurs impossible dans ma méthode car l’enfant doit d’abord construire activement les CCD et les nombres avant de pouvoir les utiliser ! Et la construction implique le comptage qui, lui, commence nécessairement par le premier 1.

Il ne faut donc surtout pas apprendre à l’enfant qu’une main c’est 5, avant qu’il n’ait pu en effectuer la construction !! Autrement on risque d’aboutir à un simple numéro ou à une simple constellation comme sur les dés ou les dominos.

Avec 5 nous entrons vraiment dans le nombreux. Le subitizing, la saisie quasi-instantanée des petites quantités (sans le recours au comptage) va au maximum jusqu’à 4.  Il nous est impossible de lire IIIII d’un seul coup, sans la moindre hésitation. Même IIII (avant l’introduction du principe soustractif) était déjà difficile et a été remplacé par IV dans les chiffres romains. Le V n’est, selon différents experts, rien d’autre qu’une main stylisée. Pour voir 5 ou plus d’éléments d’un seul coup, il faut les présenter d’une manière organisée en constellations spéciales ou faire comme les joueurs de cartes : IIII.

Comme certains hommes l’ont probablement vu depuis la nuit des temps, l’enfant peut faire l’expérience que l’entrée relativement rapide dans le nombreux ne peut réussir que grâce à la magie de l’unification assurée par le cops, notamment par les doigts. Le premier « nombreux »  se voit unifié par 1 main.

Cette unification fait que les enfants parviennent à utiliser la CCD de 5 avec beaucoup plus de facilité que les CCD de 4 et même de 3. Ainsi, pour retirer 5 de 6, 7, … , il suffit de retirer 1main ! Pour ajouter 5, il suffit d’ajouter 1 main et  de lire le résultat.

Chez beaucoup de peuples 5 a servi de base : 6, 7, … n’étant alors rien  d’autre que 5 et 1, 5 et 2,…  J’utilise 5 comme demi-base permettant de construire rapidement les nombres jusqu’à 10, 6 étant 5 (1 main) et 1doigt, etc.

La CCD de 5 (1 main) est de loin la plus facile à mémoriser, à lire, à manipuler, etc. Très différente d’une simple constellation sur un dé ou sur un domino, la CCD de 5, comme toutes les CCD, fait appel à tous les sens, notamment à la proprioception.  Elle permet ainsi  une intériorisation et une automatisation rapides.

Vu sa facilité d’utilisation alors qu’il introduit au nombreux, 5 permet d’aborder une énorme variété de  problèmes intéressants. L’enfant peut les modéliser et résoudre, en se détachant toujours plus du concret.   

Il est donc conseillé d’effectuer au plus vite les constructions jusqu’à 5 et d’utiliser la CCD de 5. Si, par exemple, l’enfant doit effectuer comme devoir scolaire 9 - 6, il vaut mieux commencer par 9 - 5, la CCD de 9 (1 main et  4doigts) - la CCD de 5 (1 main). C’est du calcul contrairement on recul pas à pas sur la ligne numérique !

La calculatrice-doigts (calculatrice) effectue quasi automatiquement tous les calculs où 5 intervient. Ainsi, 5 + 3 ou la CCD de 5 et celle de 3 donnent  la CCD de 8.

7 + 5 ou 5 + 7  donnent   +    

                                                         10                      2

Les 2 mains forment 10 (ce qui se réalise vite même inconsciemment) et le tout est donc dix- deux qui s’écrit 12 et se dit douze en français. En ce sens dix-sept, dix-huit et dix-neuf où le « dix » devient explicite, sont plus faciles à comprendre.

Même pour les « petits calculs », il faut proscrire le comptage. À cet effet, il est nécessaire de passer par la « cinquaine » (la demi-base : on remplit d’abord la première main). Exemple :

 Ce qui donne la CCD de 7.

13 - 8  donne  la CCD de 5.  Avec un peu d’habitude, l’enfant « sent » quasi directement la solution. Vu la rapidité avec laquelle il la trouve, nous pouvons conclure qu’il ne fait pas nécessairement le raisonnement que  2 mains et 3 doigts  - 1 main et 3 doigts = 1 main.    

S’il fait le décomptage un par un sur la ligne numérique, il mettra bien plus longtemps ! La ligne ou file numérique induit le comptage et obstrue même la voie qui mène au calcul.

Il est aussi essentiel de noter qu’on ne calcule pas les doigts mais on calcule avec les doigts pour résoudre un problème : j’ai reçu 13 bonbons, j’en ai mangé 8, combien en restent-ils dans la boite qui, elle, est fermée pour éviter le comptage.  L’enfant calcule combien de bonbons, et non de doigts, lui restent ! Il peut ensuite vérifier par le comptage-vérification.